Links

志望者，志望検討者の方へ

本ページは卒研配属や院試で志望を検討頂いている方向けのページです．

どのような研究をしているのか？

本研究室では，主に深層学習と情報統計力学をメインとして様々な研究を行っています． 以下では，その2つに関して簡単にご紹介します．

深層学習（深層展開）

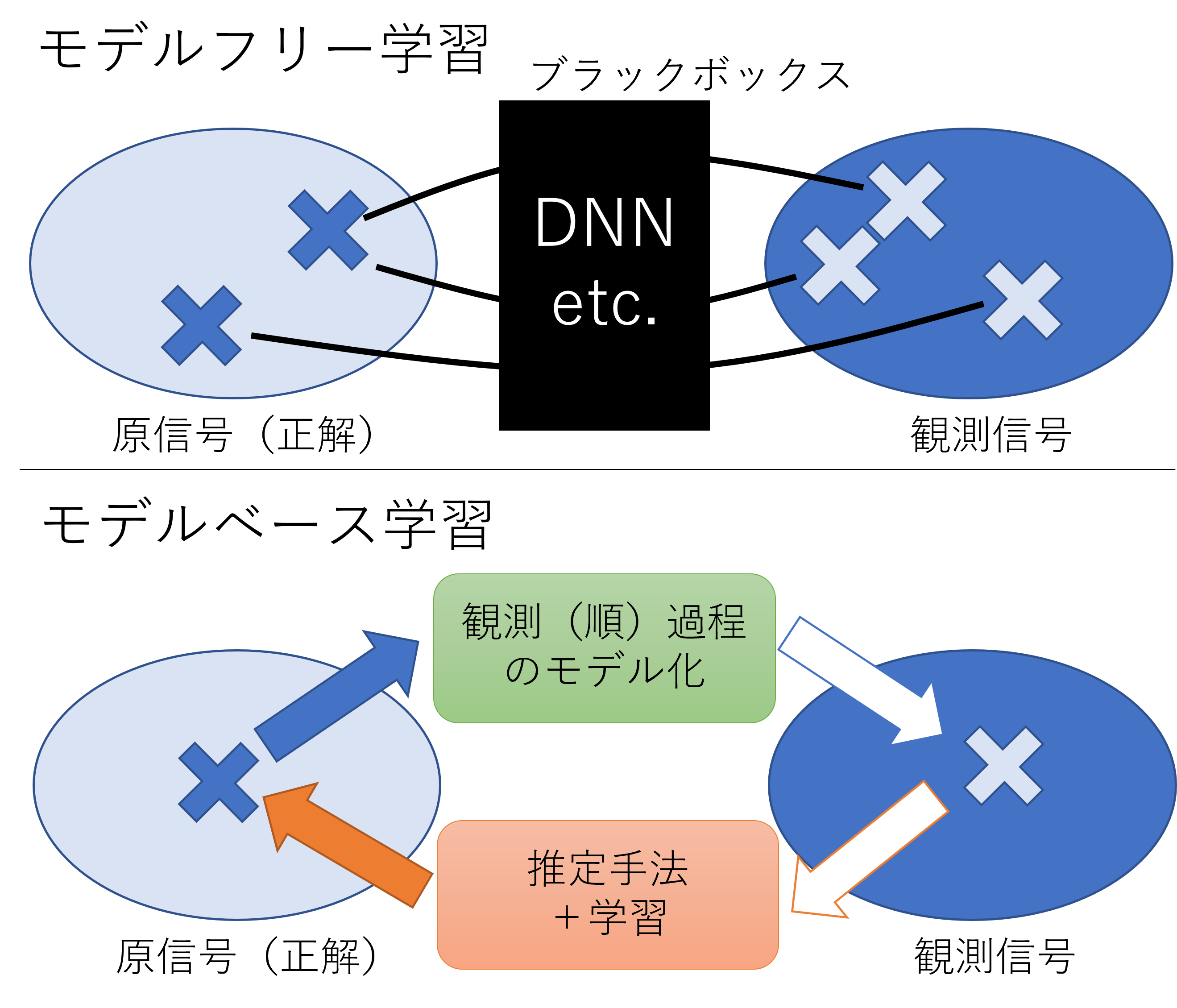
我々のグループでは，深層学習の中でも「深層展開」と呼ばれる手法に特に注目して研究しています． 通常の深層ニューラルネットワークは学習データの入出力に応じたブラックボックス関数を学習するモデルフリー学習と呼ばれるものが多いです． 一方，深層展開では，（学習に基づかない信号処理手法と同様に）学習データの入出力間に何らかの数理モデルを仮定し，それを解く反復アルゴリズムを学習によって改善することを狙いとします（下図参照）． これにより，

(1) 様々な数理モデルに対して開発されてきたアルゴリズムを使用可能，

(2) モデルフリー学習と比較して学習パラメタ数や学習コストを大幅に削減可能，

(3) アルゴリズムの性能を改善可能，

(4) 学習パラメタの意味が解釈可能，

など様々な利点があります．．

具体的な方向性としては，

• 信号処理（無線通信等）や最適化における具体的な深層展開型アルゴリズムの提案
• 新規な学習可能アルゴリズム設計による，深層展開の適用範囲の拡大(サンプラー，量子アルゴリズム etc.)
• 深層展開の学習結果や性能改善の理論的な検証

などが挙げられます．

情報統計力学

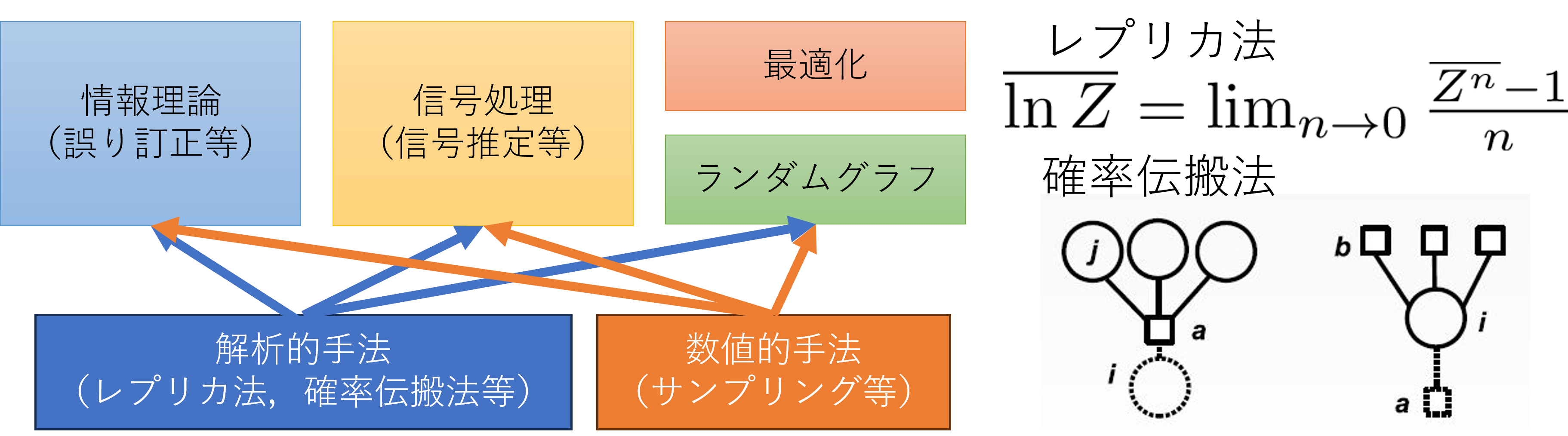
統計力学は物理学の1分野であり，物理系の方なら分配関数やボルツマン分布，平均場近似という言葉を聞いたことがあるでしょう． 実は，これらの概念は分子運動や磁性体の振る舞いを理解するだけでなく，ネットワーク上の各種問題（組合せ最適化，感染症モデルetc.），信号処理（圧縮センシング等の信号推定），情報理論（誤り訂正符号等），ニューラルネットワーク，量子計算等へ適用可能であり，様々な目覚ましい成果を上げてきました（下図）． 物理に馴染みのない方に向けて書き直すと，上記の様々な分野の問題やそこで使われている確率的な情報処理手法が物理学の概念で綺麗につながっており，水が氷になるような「相転移現象」がこれらの（関係なさそうな）様々な対象に共通して現れるという不思議なものの見方を提供する分野になっています．物理学の諸手法が情報分野へ応用でき，新たな視点や解決法を提供可能な点が魅力です．

本研究室では，理論的アプローチ（平均場近似）と数値的アプローチ（モンテカルロ法等のサンプリング）の両面からこれらの問題にアタックしています．

FAQ

（以下は，あくまで本研究室の話であり，所属する系，学院の他研究室とは異なる回答である可能性があります．また，その他のご質問はお気軽にお尋ねください．）

• 第〇志望だが志望してよいか？

ご検討ありがとうございます．第何志望でもかまいません． ただし，修士志望の方で第1志望の場合は事前に必ずメール等でご連絡ください． また，第2志望以下の場合でも志望理由をある程度しっかり（＝具体的に）持たれることをお勧めします． いずれにしてもご質問や教員の雰囲気（大事な要素です）を知りたい方はメールで一度お問い合わせください（学部生の方は第〇志望と明記しないようお願いします）．

また，内定された方はすぐに高邉までご一報ください．

• 研究室のスケジュールは？

各学生とは1週間に1回の1対1での進捗報告/議論 (B4の夏学期はゼミ) があり，研究室全体で週1回の全体報告会があります． 全体報告会では，学生の持ち回りで自分の研究の話や論文紹介，勉強したこと等を報告，議論し合います． また，学生が自主ゼミ等を行っている場合もあります．ちなみに，コアタイムは設けていません．

• 研究テーマについて

研究テーマを学生に任せる研究室，与える研究室両方に所属した経験がありますので，学生さんの適性を見つつ柔軟に対応します． 学生さんのやりたいテーマがある場合はそれをベースに研究計画を立てるお手伝いをします（あまりに高邉の専門外ならば不可能な場合もありますので事前相談必須です）．

• 研究室に所属する前にどんなことができていればよいか？

以下の2点が推奨されます．

(1) 基本的な線形代数，確率論，数理最適化（連続，離散），数理統計学等の知識があること．

(2) 基本的なPythonプログラミングが可能なこと．

逆にいえば，信号処理や物理学の詳細に関する知識は問いません（あればなお良いですが）．

• 物理/情報/他分野・他大学の出身だが志望可能か？（修士）

はい，可能です．本研究室の院生のうち内部生は約半数で，残りは様々な経歴（数学科，商学部出身等）の方です． 反対に，B4で本研究室に配属されたからと言って修士も本研究室に自動的に進めるわけではありません（院試次第）． ただし，他大学の方は数理・計算科学系の入試情報や院試問題の傾向（過去問はこちら）について志望する前にしっかりご確認ください．

• 学会等へ行く機会はあるか？（修士）

可能な限り修士の間に少なくとも1回は学会や研究会で自分の研究を発表する機会を提供します． 実際には2回以上発表/参加される方が多いです． 研究会としては，電子情報通信学会（情報系）や日本物理学会（物理系）が多いです． 修士１年時の発表で研究会賞を受賞した実績もあります．

• 修士で就職するつもりだが問題ないか？博士課程に進みたいが大丈夫か？

勿論どちらでも結構です．バイトやインターン・就活等で研究がある程度ストップ/遅延しても問題ないような進捗管理に協力します． 博士進学希望の方は諸々の戦略を立てて研究を進めていけるよう協力します．

• 就職先は？

出来立ての研究室ということもあって，サンプルが少ないので研究室としての実績を公開する予定はありません． 系としての実績はこちらをご覧ください．

• 1学年で研究室には何人まで配属可能か？

様々な要因で変動することがあるので一概に何人かは申し上げられません．

• その他

一度こちら（および当該年度の類似ページ）をご覧ください．よくある質問がまとめられています．